Epidemien modellieren

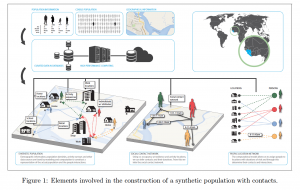
Zu den Hoffnungsträgern der gegenwärtigen Situation (und jedes vergleichbaren, durch eine Epidemie verursachten Ausnahmezustands) gehören die statistischen und epidemiologischen Wissenschaften, die ein solches Geschehen am Computer modellieren. Die mathematisch errechneten Szenarien funktionieren ähnlich wie die Wettervorhersage oder die Forecasts der Finanzindustrie. Ihre Basis sind Wahrscheinlichkeiten, die entlang bestimmter mathematischer (oder wohl besser: stochastischer) Parameter, in deren Konstruktion historische Daten, Vorannahmen und Verhaltenserwartungen eingehen, in Verlaufsdiagramme und – mehr oder weniger anschauliche – Szenarien übersetzt werden. Die visuelle Form dieser Szenarien kann vom „einfachen“ Koordinatennetz bis zu dreidimensionalen Kompositbildern wie dem oben gezeigten (aus einer Studie über „synthetische Populationen“ zur Modellierung von Epidemien aus dem Network Dynamics and Simulation Science Laboratory – der Name dieses Labs ist schon Programm – an der Virginia Tech [Blacksburg, VA]) reichen. Die Epidemiologie baut ihre Szenarien, ähnlich wie dies in anderen (z.B. wirtschaftlichen, logistischen, organisationsrelevanten) Kontexten der Fall ist, auf der Grundlage bestimmter Theorien und Methodologien, die in den wissenschaftlichen Communities ein Gegenstand ständiger Diskussion und Erneuerung sind.

Die Planungs- und Organisationswissenschaften haben durch Big Data und AI einen erheblichen Entwicklungssprung vollzogen. Deep Learning-Algorithmen werden kontinuierlich durch die Auswertung auch und gerade von social media-Daten neu parametrisiert. Die Überwachung sozialen Verhaltens wird zur Voraussetzung der Modellierung des Verlaufs von Infektionskrankheiten und damit auch zur Entscheidungs- und Rechtfertigungsgrundlage der zu ergreifenden politischen und polizeilichen Maßnahmen. Trotzdem liegen dem Erfolg der algorithmischen Routinen dieser Modellierungen und ihrer Vorhersagen weiterhin mathematische Formeln zugrunde, die in den Fachpapers dann gelegentlich quasi-visuelle Gestalt annehmen.

Eine für die epidemiologische Modellierung besonders zentrale Formel ist die der SEIR-Progression, wonach „susceptible individuals in disease class S enter disease class E on exposure to a pathogen (i.e., infected but not yet infectious themselves)“ und „individuals in class E then transfer, after a period of latency, into the class of infectious individuals, I, only to transfer to a recovered or removed class R.“

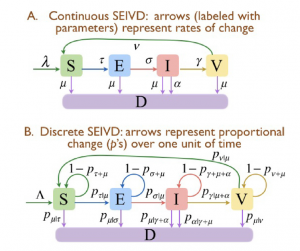
Flow diagrams for the basic SEIVD continuous (A) and discrete (B) time models with transition rates τ, σ, γ and ν from disease classes S to E, E to I, I to V
and V back to S, respectively. (Wayne M. Getz et al, Modeling epidemics: A primer and Numerus Model Builder implementation, Epidemics, 25 [2018], 9–19)

Die Kunst der veranschaulichenden Darstellung liegt darin, die Entwicklung und Ausbreitung, die Veränderungsraten der Epidemie (und deren Steigerung oder Absenkung) plausibel zu visualisieren, ohne dadurch das mathematische Funktionieren der Formel zu hintertreiben. So entstehen hybride Bilderformeln oder Formelbilder, die unter der Last der ihnen zugemuteten Komplexität und Abstraktheit oft erkennbar leiden.

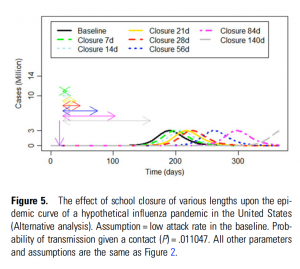
Was besonders Eltern, Kinder und Lehrer*innen heute interessieren dürfte, sind Studien zur Effizienz von Schulschließungen während einer Epidemie wie der jetzigen. Eine 2015 veröffentlichte amerikanische Studie zu Influenza-Pandemien kam zu dem Schluss: „School closures may delay the epidemic peak of the next influenza pandemic, but whether school closure can delay the peak until pandemic vaccine is ready to be deployed is uncertain.“

aus: Isaac Chun-Hai Fung et al., Modeling the Effect of School Closures in a Pandemic Scenario: Exploring Two Different Contact Matrices, Clinical Infectious Diseases 60 (2015)

Um die Wechselwirkung zwischen Schulschließungen und dem Zeitpunkt der Höhepunkte einer Epidemie zu untersuchen, baute das Forscher*innen-Team „a deterministic susceptible-infected-recovered model of influenza transmission“, indem die Bevölkerung (hier: der USA) in vier Altersgruppen unterteilt wurde und sogenannte Kontaktmatrizen (contact matrices) zur Modellierung der durchschnittlichen Anzahl übertragender, aber nicht physischer Kontakte erstellt wurden. Die Ergebnisse waren einigermaßen ernüchternd: „For every week of school closure at day 5 of introduction and a 30% clinical attack rate scenario, epidemic peak would be delayed by approximately 5 days. For a 15% clinical attack rate scenario, 1 week closure would delay the peak by 9 days. Closing schools for less than 84 days (12 weeks) would not, however, reduce the estimated total number of cases.“ Nur wenn ein Impfstoff in die Gleichung eingeführt wird, verändern sich die Prognosen zum Positiven: „Unless vaccine is available early, school closure alone may not be able to delay the peak until vaccine is ready to be deployed. Conversely, if vaccination begins quickly, school closure may be helpful in providing the time to vaccinate school-aged children before the pandemic peaks.“

Im dazugehörigen Diagramm (siehe oben) wurde eine Fülle von Varianten des Szenarios verarbeitet, allerdings ist das generierte Koordinaten-Bild trotz seiner Mehrfarbigkeit für das ungeübte Auge eher wenig aussagekräftig – zu gleichmäßig, ohne dramatische Ausschläge schwappen die Wellen/Kurven, so als wäre diese Brandung völlig unter Kontrolle.

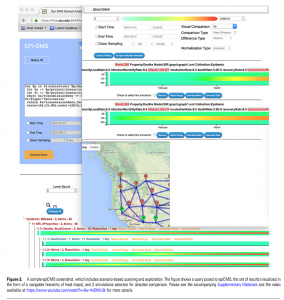
Die Realsituation des Desktops einer Epidemiologin heute dürfte ohnehin eher so aussehen wie in dieser Abbildung aus einem Paper zu Datenmanagement und Entscheidungsfindung, das auf der Grundlage von Ausbreitungs-Simulationen geschrieben wurde: eine Vielzahl gleichzeitig geöffneter Fenster, die – siehe das Prinzip „dashboard“ – geografisches Kartenmaterial, Spektraldiagramme, Textfelder usw. offeriert und das Heil (die Heilung?) in der Schichtung, der Überlappung sucht. TH

Sicong Liu et al., epiDMS: Data Management and Analytics for Decision-Making From Epidemic Spread Simulation Ensembles, The Journal of Infectious Diseases 214 (2016) (Suppl 4)